Scope

Feature selection is the process of finding an optimal set of features to improve the performance, interpretability and robustness of machine learning algorithms. In this article, we introduce the Shadow Variable Search algorithm which is a wrapper method for feature selection. Wrapper methods iteratively add features to the model that optimize a performance measure. As an example, we will search for the optimal set of features for a support vector machine on the Pima Indian Diabetes data set. We assume that you are already familiar with the basic building blocks of the mlr3 ecosystem. If you are new to feature selection, we recommend reading the feature selection chapter of the mlr3book first. Some knowledge about mlr3pipelines is beneficial but not necessary to understand the example.

Shadow Variable Search

Adding shadow variables to a data set is a well-known method in machine learning (Wu, Boos, and Stefanski 2007; Thomas et al. 2017). The idea is to add permutated copies of the original features to the data set. These permutated copies are called shadow variables or pseudovariables and the permutation breaks any relationship with the target variable, making them useless for prediction. The subsequent search is similar to the sequential forward selection algorithm, where one new feature is added in each iteration of the algorithm. This new feature is selected as the one that improves the performance of the model the most. This selection is computationally expensive, as one model for each of the not yet included features has to be trained. The difference between shadow variable search and sequential forward selection is that the former uses the selection of a shadow variable as the termination criterion. Selecting a shadow variable means that the best improvement is achieved by adding a feature that is unrelated to the target variable. Consequently, the variables not yet selected are most likely also correlated to the target variable only by chance. Therefore, only the previously selected features have a true influence on the target variable.

mlr3fselect is the feature selection package of the mlr3 ecosystem. It implements the shadow variable search algorithm. We load all packages of the ecosystem with the mlr3verse package.

library(mlr3verse)

We retrieve the shadow variable search optimizer with the fs() function. The algorithm has no control parameters.

optimizer = fs("shadow_variable_search")

Task and Learner

The objective of the Pima Indian Diabetes data set is to predict whether a person has diabetes or not. The data set includes 768 patients with 8 measurements (see Figure 1).

task = tsk("pima")

Code

library(ggplot2)
library(data.table)

data = melt(as.data.table(task), id.vars = task$target_names, measure.vars = task$feature_names)

ggplot(data, aes(x = value, fill = diabetes)) +
  geom_density(alpha = 0.5) +
  facet_wrap(~ variable, ncol = 8, scales = "free") +
  scale_fill_viridis_d(end = 0.8) +
  theme_minimal() +
  theme(axis.title.x = element_blank())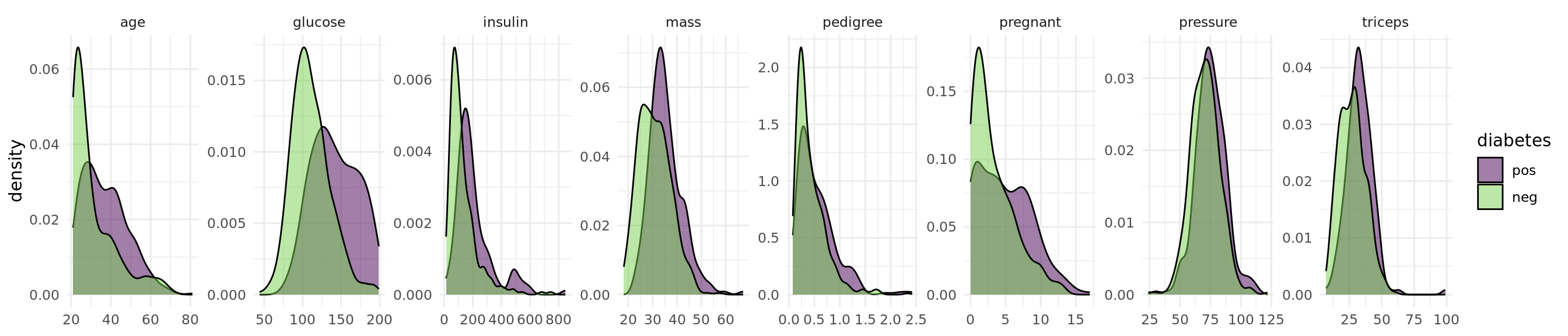

Figure 1: Distribution of the features in the Pima Indian Diabetes data set.

The data set contains missing values.

task$missings()

diabetes      age  glucose  insulin     mass pedigree pregnant pressure  triceps 
       0        0        5      374       11        0        0       35      227

Support vector machines cannot handle missing values. We impute the missing values with the histogram imputation method.

learner = po("imputehist") %>>% lrn("classif.svm", predict_type = "prob")

Feature Selection

Now we define the feature selection problem by using the fsi() function that constructs an FSelectInstanceSingleCrit. In addition to the task and learner, we have to select a resampling strategy and performance measure to determine how the performance of a feature subset is evaluated. We pass the "none" terminator because the shadow variable search algorithm terminates by itself.

instance = fsi(
  task = task,
  learner = learner,
  resampling = rsmp("cv", folds = 3),
  measures = msr("classif.auc"),
  terminator = trm("none")
)

We are now ready to start the shadow variable search. To do this, we simply pass the instance to the $optimize() method of the optimizer.

optimizer$optimize(instance)

    age glucose insulin mass pedigree pregnant pressure triceps                  features classif.auc
1: TRUE    TRUE   FALSE TRUE     TRUE    FALSE    FALSE   FALSE age,glucose,mass,pedigree    0.835165

The optimizer returns the best feature set and the corresponding estimated performance.

Figure 2 shows the optimization path of the feature selection. The feature glucose was selected first and in the following iterations age, mass and pedigree. Then a shadow variable was selected and the feature selection was terminated.

Code

library(data.table)
library(ggplot2)
library(mlr3misc)
library(viridisLite)

data = as.data.table(instance$archive)[order(-classif.auc), head(.SD, 1), by = batch_nr][order(batch_nr)]
data[, features := map_chr(features, str_collapse)]
data[, batch_nr := as.character(batch_nr)]

ggplot(data, aes(x = batch_nr, y = classif.auc)) +
  geom_bar(
    stat = "identity",
    width = 0.5,
    fill = viridis(1, begin = 0.5),
    alpha = 0.8) +
  geom_text(
    data = data,
    mapping = aes(x = batch_nr, y = 0, label = features),
    hjust = 0,
    nudge_y = 0.05,
    color = "white",
    size = 5
    ) +
  coord_flip() +
  xlab("Iteration") +
  theme_minimal()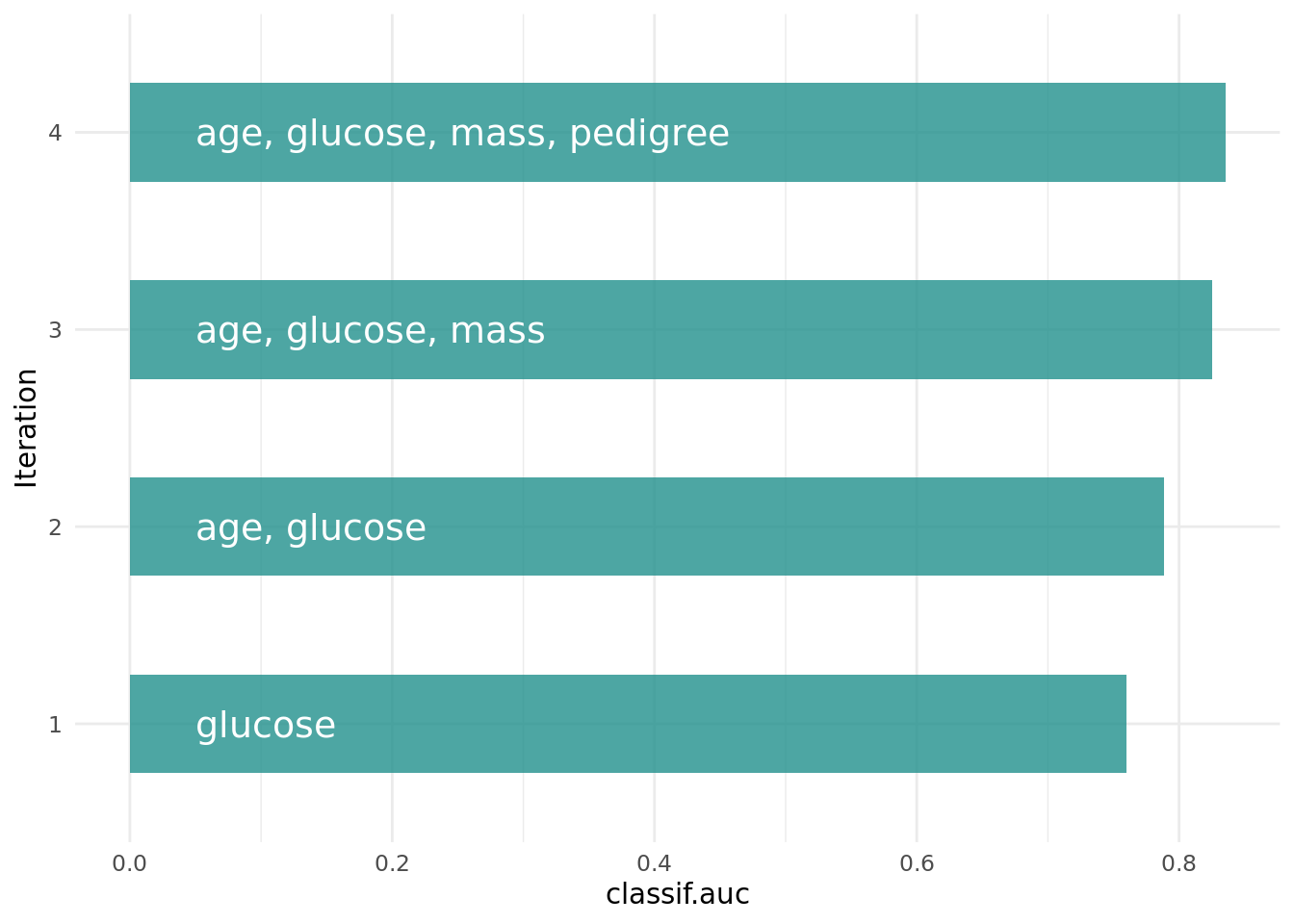

Figure 2: Optimization path of the shadow variable search.

The archive contains all evaluated feature sets. We can see that each feature has a corresponding shadow variable. We only show the variables age, glucose and insulin and their shadow variables here.

as.data.table(instance$archive)[, .(age, glucose, insulin, permuted__age, permuted__glucose, permuted__insulin, classif.auc)]

      age glucose insulin permuted__age permuted__glucose permuted__insulin classif.auc
 1:  TRUE   FALSE   FALSE         FALSE             FALSE             FALSE   0.6437052
 2: FALSE    TRUE   FALSE         FALSE             FALSE             FALSE   0.7598155
 3: FALSE   FALSE    TRUE         FALSE             FALSE             FALSE   0.4900280
 4: FALSE   FALSE   FALSE         FALSE             FALSE             FALSE   0.6424026
 5: FALSE   FALSE   FALSE         FALSE             FALSE             FALSE   0.5690107
---                                                                                    
54:  TRUE    TRUE   FALSE         FALSE             FALSE             FALSE   0.8266713
55:  TRUE    TRUE   FALSE         FALSE             FALSE             FALSE   0.8063568
56:  TRUE    TRUE   FALSE         FALSE             FALSE             FALSE   0.8244232
57:  TRUE    TRUE   FALSE         FALSE             FALSE             FALSE   0.8234605
58:  TRUE    TRUE   FALSE         FALSE             FALSE             FALSE   0.8164784

Final Model

The learner we use to make predictions on new data is called the final model. The final model is trained with the optimal feature set on the full data set. We subset the task to the optimal feature set and train the learner.

task$select(instance$result_feature_set)
learner$train(task)

The trained model can now be used to predict new, external data.

Conclusion

The shadow variable search is a fast feature selection method that is easy to use. More information on the theoretical background can be found in Wu, Boos, and Stefanski (2007) and Thomas et al. (2017). If you want to know more about feature selection in general, we recommend having a look at our book.

References

Thomas, Janek, Tobias Hepp, Andreas Mayr, and Bernd Bischl. 2017. “Probing for Sparse and Fast Variable Selection with Model-Based Boosting.” Computational and Mathematical Methods in Medicine 2017 (July): e1421409. https://doi.org/10.1155/2017/1421409.

Wu, Yujun, Dennis D Boos, and Leonard A Stefanski. 2007. “Controlling Variable Selection by the Addition of Pseudovariables.” Journal of the American Statistical Association 102 (477): 235–43. https://doi.org/10.1198/016214506000000843.