Survival modeling in mlr3 using Bayesian Additive Regression Trees (BART)

Demonstrate use of survival BART on the lung dataset via mlr3proba and distr6.

Author

John Zobolas

Published

October 25, 2023

Intro

Here are some interesting reads regarding BART:

We incorporated the survival BART model in mlr3extralearners and in this tutorial we will demonstrate how we can use packages like mlr3, mlr3proba and distr6 to more easily manipulate the output predictions to assess model convergence, validate our model (via several survival metrics), as well as perform model interpretation via PDPs (Partial Dependence Plots).

Libraries

library(mlr3extralearners)
library(mlr3pipelines)
library(mlr3proba)
library(distr6)
library(BART) # 2.9.4
library(dplyr)
library(tidyr)
library(tibble)
library(ggplot2)

Data

We will use the Lung Cancer Dataset. We convert the time variable from days to months to ease the computational burden:

task_lung = tsk('lung')

d = task_lung$data()
# in case we want to select specific columns to keep
# d = d[ ,colnames(d) %in% c("time", "status", "age", "sex", "ph.karno"), with = FALSE]
d$time = ceiling(d$time/30.44)
task_lung = as_task_surv(d, time = 'time', event = 'status', id = 'lung')
task_lung$label = "Lung Cancer"
Note
  1. The original BART implementation supports categorical features (factors). This results in different importance scores per each dummy level which doesn’t work well with mlr3. So features of type factor or character are not allowed and we leave it to the user to encode them as they please.
  2. The original BART implementation supports features with missing values. This is totally fine with mlr3 as well! In this example, we impute the features to show good ML practice.

In our lung dataset, we encode the sex feature and perform model-based imputation with the rpart regression learner:

po_encode = po('encode', method = 'treatment')
po_impute = po('imputelearner', lrn('regr.rpart'))
pre = po_encode %>>% po_impute
task = pre$train(task_lung)[[1]]
task
<TaskSurv:lung> (168 x 9): Lung Cancer
* Target: time, status
* Properties: -
* Features (7):
  - int (6): age, meal.cal, pat.karno, ph.ecog, ph.karno, wt.loss
  - dbl (1): sex

No missing values in our data:

task$missings()
     time    status       age  meal.cal pat.karno   ph.ecog  ph.karno   wt.loss       sex 
        0         0         0         0         0         0         0         0         0

We partition the data to train and test sets:

set.seed(42)
part = partition(task, ratio = 0.9)

Train and Test

We train the BART model and predict on the test set:

# default `ndpost` value: 1000. We reduce it to 50 to speed up calculations in this tutorial
learner = lrn("surv.bart", nskip = 250, ndpost = 50, keepevery = 10, mc.cores = 10)
learner$train(task, row_ids = part$train)
p = learner$predict(task, row_ids = part$test)
p

See more details about BART’s parameters on the online documentation.

distr

What kind of object is the predicted distr?

p$distr
Arrdist(17x30x50)
Arrdist dimensions:
  1. Patients (observations)
  2. Time points (months)
  3. Number of posterior draws

Actually the $distr is an active R6 field - this means that some computation is required to create it. What the prediction object actually stores internally is a 3d survival array (can be used directly with no performance overhead):

dim(p$data$distr)
[1] 17 30 50

This is a more easy-to-understand and manipulate form of the full posterior survival matrix prediction from the BART package ((R. Sparapani, Spanbauer, and McCulloch 2021), pages 34-35).

Warning

Though we have optimized with C++ code the way the Arrdist object is constructed, calling the $distr field can be computationally taxing if the product of the sizes of the 3 dimensions above exceeds ~1 million. In our case, \(23 \times 31 \times 50 = 35650\) so the conversion to an Arrdist via $distr will certainly not create performance issues.

An example using the internal prediction data: get all the posterior probabilities of the 3rd patient in the test set, at 12 months (1 year):

p$data$distr[3, 12, ]
 [1] 0.16682639 0.52846967 0.51057138 0.23143445 0.24949314 0.23818569 0.28702429 0.39494813 0.68549420 0.38617165
[11] 0.18528656 0.18365059 0.58371359 0.34762244 0.30502214 0.20621051 0.73117066 0.37176522 0.44852366 0.48714300
[21] 0.13227459 0.36120922 0.04110908 0.08701728 0.26405672 0.13075270 0.33063856 0.71372303 0.28818814 0.43886058
[31] 0.16152343 0.11132334 0.09516388 0.26125352 0.16578149 0.33411388 0.32607511 0.43967968 0.25908991 0.21763759
[41] 0.47965258 0.50324377 0.13649939 0.40579983 0.29247802 0.09903617 0.56096633 0.26853225 0.20253541 0.42479851

Working with the $distr interface and Arrdist objects is very efficient as we will see later for predicting survival estimates.

Tip

In survival analysis, \(S(t) = 1 - F(t)\), where \(S(t)\) the survival function and \(F(t)\) the cumulative distribution function (cdf). The latter can be interpreted as risk or probability of death up to time \(t\).

We can verify the above from the prediction object:

surv_array = 1 - distr6::gprm(p$distr, "cdf") # 3d array
all_equal(p$data$distr, surv_array)
Warning: `all_equal()` was deprecated in dplyr 1.1.0.
ℹ Please use `all.equal()` instead.
ℹ And manually order the rows/cols as needed
`y` must be a data frame.

crank

crank is the expected mortality (Sonabend, Bender, and Vollmer 2022) which is the sum of the predicted cumulative hazard function (as is done in random survival forest models). Higher values denote larger risk. To calculate crank, we need a survival matrix. So we have to choose which 3rd dimension we should use from the predicted survival array. This is what the which.curve parameter of the learner does:

learner$param_set$get_values()$which.curve
[1] 0.5

The default value (\(0.5\) quantile) is the median survival probability. It could be any other quantile (e.g. \(0.25\)). Other possible values for which.curve are mean or a number denoting the exact posterior draw to extract (e.g. the last one, which.curve = 50).

Feature importance

Default score is the observed count of each feature in the trees (so the higher the score, the more important the feature):

learner$param_set$values$importance
[1] "count"
learner$importance()
      sex   wt.loss  ph.karno  meal.cal pat.karno       age   ph.ecog 
     8.94      8.22      8.16      7.74      6.44      6.28      6.28

MCMC Diagnostics

BART uses internally MCMC (Markov Chain Monte Carlo) to sample from the posterior survival distribution. We need to check that MCMC has converged, meaning that the chains have reached a stationary distribution that approximates the true posterior survival distribution (otherwise the predictions may be inaccurate, misleading and unreliable).

We use Geweke’s convergence diagnostic test as it is implemented in the BART R package. We choose 10 random patients from the train set to evaluate the MCMC convergence.

# predictions on the train set
p_train = learner$predict(task, row_ids = part$train)

# choose 10 patients from the train set randomly and make a list
ids = as.list(sample(length(part$train), 10))

z_list = lapply(ids, function(id) {
  # matrix with columns => time points and rows => posterior draws
  post_surv = 1 - t(distr6::gprm(p_train$distr[id], "cdf")[1,,])
  BART::gewekediag(post_surv)$z # get the z-scores
})

# plot the z scores vs time for all patients
dplyr::bind_rows(z_list) %>%
  tidyr::pivot_longer(cols = everything()) %>%
  mutate(name = as.numeric(name)) %>%
  ggplot(aes(x = name, y = value)) +
  geom_point() +
  labs(x = "Time (months)", y = "Z-scores") +
  # add critical values for a = 0.05
  geom_hline(yintercept = 1.96, linetype = 'dashed', color = "red") +
  geom_hline(yintercept = -1.96, linetype = 'dashed', color = "red") +
  theme_bw(base_size = 14)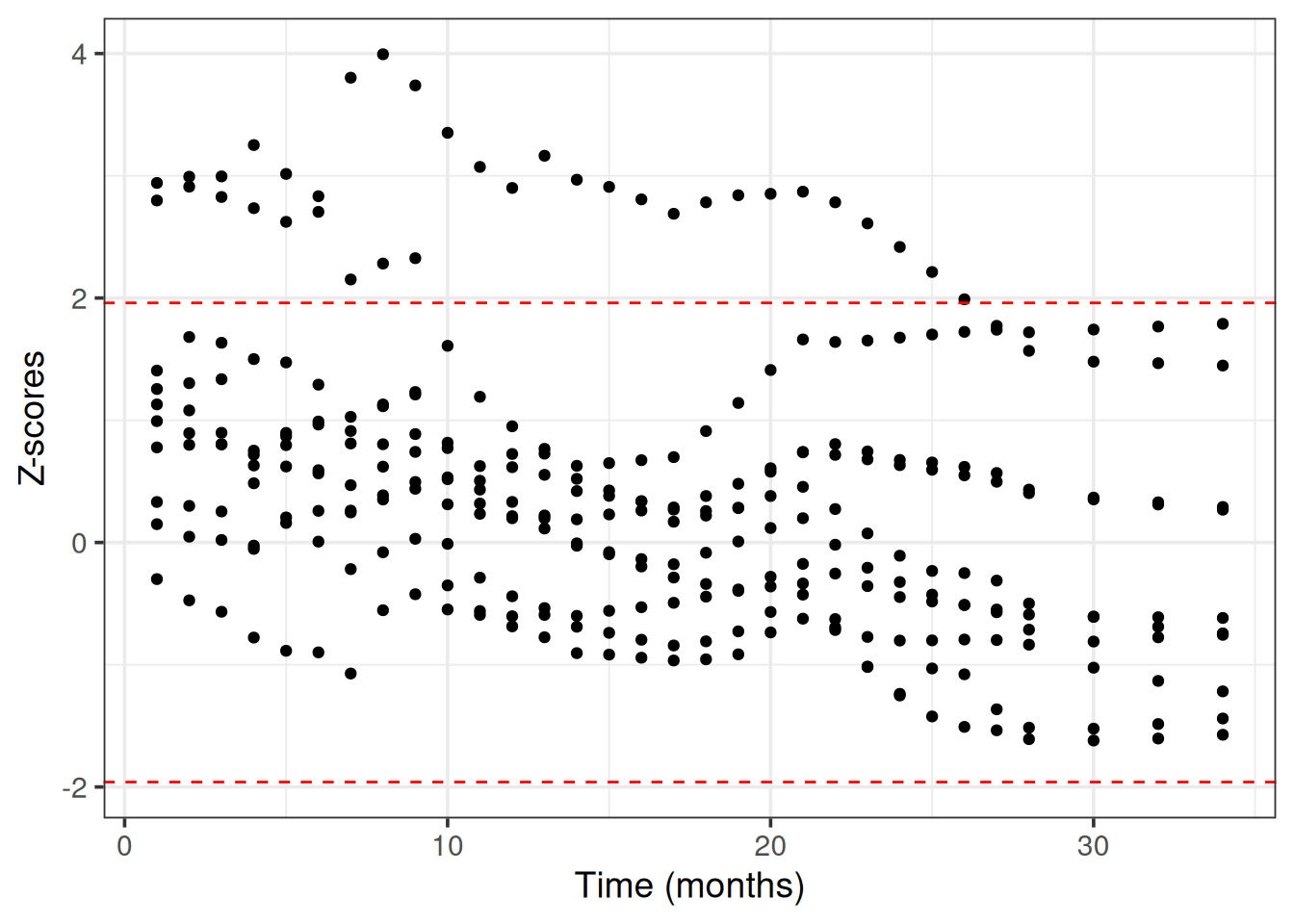

Geweke plot for MCMC diagnostics. Z-scores for the difference in the mean survival prediction between the first 10% and last 50% part of a Markov chain. The predictions are taken from 10 random patients in the train set. Red lines indicate the a = 0.05 critical line. Only a few z-scores exceed the 95% limits so we conclude that convergence has been attained.

Performance (test set)

We will use the following survival metrics:

  1. Integrated Brier Score (requires a survival distribution prediction - distr)
  2. Uno’s C-index (requires a continuous ranking score prediction - crank)

For the first measure we will use the ERV (Explained Residual Variation) version, which standardizes the score against a Kaplan-Meier (KM) baseline (Sonabend et al. 2022). This means that values close to \(0\) represent performance similar to a KM model, negative values denote worse performance than KM and \(1\) is the absolute best possible score.

measures = list(
  msr("surv.graf", ERV = TRUE),
  msr("surv.cindex", weight_meth = "G2", id = "surv.cindex.uno")
)

for (measure in measures) {
  print(p$score(measure, task = task, train_set = part$train))
}
surv.graf 
0.1607549 
surv.cindex.uno 
      0.7120706
Note

All metrics use by default the median survival distribution from the 3d array, no matter what is the which.curve argument during the learner’s construction.

Resampling

Performing resampling with the BART learner is very easy using mlr3.

We first stratify the data by status, so that in each resampling the proportion of censored vs un-censored patients remains the same:

task$col_roles$stratum = 'status'
task$strata
       N                row_id
   <int>                <list>
1:   121       1,2,4,5,6,7,...
2:    47  3,26,49,52,62,64,...
rr = resample(task, learner, resampling = rsmp("cv", folds = 5), store_backends = TRUE)
INFO  [14:22:15.342] [mlr3] Applying learner 'surv.bart' on task 'lung' (iter 1/5)
INFO  [14:22:16.982] [mlr3] Applying learner 'surv.bart' on task 'lung' (iter 2/5)
INFO  [14:22:18.456] [mlr3] Applying learner 'surv.bart' on task 'lung' (iter 3/5)
INFO  [14:22:19.907] [mlr3] Applying learner 'surv.bart' on task 'lung' (iter 4/5)
INFO  [14:22:21.351] [mlr3] Applying learner 'surv.bart' on task 'lung' (iter 5/5)

No errors or warnings:

rr$errors
Empty data.table (0 rows and 2 cols): iteration,msg
rr$warnings
Empty data.table (0 rows and 2 cols): iteration,msg

Performance in each fold:

rr$score(measures)
   task_id learner_id resampling_id iteration   surv.graf surv.cindex.uno
    <char>     <char>        <char>     <int>       <num>           <num>
1:    lung  surv.bart            cv         1  0.06674423       0.6270652
2:    lung  surv.bart            cv         2 -0.06994762       0.5789767
3:    lung  surv.bart            cv         3 -0.05637324       0.5880529
4:    lung  surv.bart            cv         4  0.02718982       0.6126352
5:    lung  surv.bart            cv         5 -0.08941180       0.5695597
Hidden columns: task, learner, resampling, prediction_test

Mean cross-validation performance:

rr$aggregate(measures)
      surv.graf surv.cindex.uno 
    -0.02435972      0.59525794

Uncertainty Quantification in Survival Prediction

We will choose two patients from the test set and plot their survival prediction posterior estimates.

Let’s choose the patients with the worst and the best survival time:

death_times = p$truth[,1]
sort(death_times)
 [1]  2  4  6  6  6  7  8  9 10 10 10 10 13 15 15 19 22
worst_indx = which(death_times == min(death_times))[1] # died first
best_indx  = which(death_times == max(death_times))[1] # died last

patient_ids = c(worst_indx, best_indx)
patient_ids # which patient IDs
[1] 12  9
death_times = death_times[patient_ids]
death_times # 1st is worst, 2nd is best
[1]  2 22

Subset Arrdist to only the above 2 patients:

arrd = p$distr[patient_ids]
arrd
Arrdist(2x30x50)

We choose time points (in months) for the survival estimates:

months = seq(1, 36) # 1 month - 3 years

We use the $distr interface and the $survival property to get survival probabilities from an Arrdist object as well as the quantile credible intervals (CIs). The median survival probabilities can be extracted as follows:

med = arrd$survival(months) # 'med' for median

colnames(med) = paste0(patient_ids, "_med")
med = as_tibble(med) %>% add_column(month = months)
head(med)
# A tibble: 6 × 3
  `12_med` `9_med` month
     <dbl>   <dbl> <int>
1    0.857   0.974     1
2    0.741   0.948     2
3    0.630   0.923     3
4    0.524   0.900     4
5    0.446   0.872     5
6    0.362   0.833     6

We can briefly verify model’s predictions: 1st patient survival probabilities on any month are lower (worst) compared to the 2nd patient.

Note that subsetting an Arrdist (3d array) creates a Matdist (2d matrix), for example we can explicitly get the median survival probabilities:

matd_median = arrd[, 0.5] # median
head(matd_median$survival(months)) # same as with `arrd`
       [,1]      [,2]
1 0.8574541 0.9736144
2 0.7409911 0.9479014
3 0.6304261 0.9226185
4 0.5236389 0.8996011
5 0.4457717 0.8721516
6 0.3620130 0.8329688

Using the mean posterior survival probabilities or the ones from the last posterior draw is also possible and can be done as follows:

matd_mean = arrd[, "mean"] # mean (if needed)
head(matd_mean$survival(months))
       [,1]      [,2]
1 0.8494062 0.9721130
2 0.7246768 0.9445261
3 0.6213767 0.9154688
4 0.5246258 0.8865332
5 0.4487428 0.8576749
6 0.3644190 0.8155328
matd_50draw = arrd[, 50] # the 50th posterior draw
head(matd_50draw$survival(months))
       [,1]      [,2]
1 0.7671943 0.9865953
2 0.5885871 0.9733703
3 0.4515607 0.9603225
4 0.3464348 0.9474497
5 0.2657828 0.9347494
6 0.1812379 0.9112550

To get the CIs we will subset the Arrdist using a quantile number (0-1), which extracts a Matdist based on the cdf. The survival function is 1 - cdf, so low and upper bounds are reversed:

low  = arrd[, 0.975]$survival(months) # 2.5% bound
high = arrd[, 0.025]$survival(months) # 97.5% bound
colnames(low)  = paste0(patient_ids, "_low")
colnames(high) = paste0(patient_ids, "_high")
low  = as_tibble(low)
high = as_tibble(high)

The median posterior survival probabilities for the two patient of interest and the corresponding CI bounds in a tidy format are:

surv_tbl =
  bind_cols(low, med, high) %>%
  pivot_longer(cols = !month, values_to = "surv",
    names_to = c("patient_id", ".value"), names_sep = "_") %>%
  relocate(patient_id)
surv_tbl
# A tibble: 72 × 5
   patient_id month    low   med  high
   <chr>      <int>  <dbl> <dbl> <dbl>
 1 12             1 0.639  0.857 0.962
 2 9              1 0.929  0.974 0.994
 3 12             2 0.398  0.741 0.925
 4 9              2 0.864  0.948 0.988
 5 12             3 0.230  0.630 0.889
 6 9              3 0.803  0.923 0.980
 7 12             4 0.133  0.524 0.828
 8 9              4 0.761  0.900 0.976
 9 12             5 0.0773 0.446 0.770
10 9              5 0.722  0.872 0.971
# ℹ 62 more rows

We draw survival curves with the uncertainty for the survival probability quantified:

my_colors = c("#E41A1C", "#4DAF4A")
names(my_colors) = patient_ids

surv_tbl %>%
  ggplot(aes(x = month, y = med)) +
  geom_step(aes(color = patient_id), linewidth = 1) +
  xlab('Time (Months)') +
  ylab('Survival Probability') +
  geom_ribbon(aes(ymin = low, ymax = high, fill = patient_id),
    alpha = 0.3, show.legend = F) +
  geom_vline(xintercept = death_times[1], linetype = 'dashed', color = my_colors[1]) +
  geom_vline(xintercept = death_times[2], linetype = 'dashed', color = my_colors[2]) +
  theme_bw(base_size = 14) +
  scale_color_manual(values = my_colors) +
  scale_fill_manual(values = my_colors) +
  guides(color = guide_legend(title = "Patient ID"))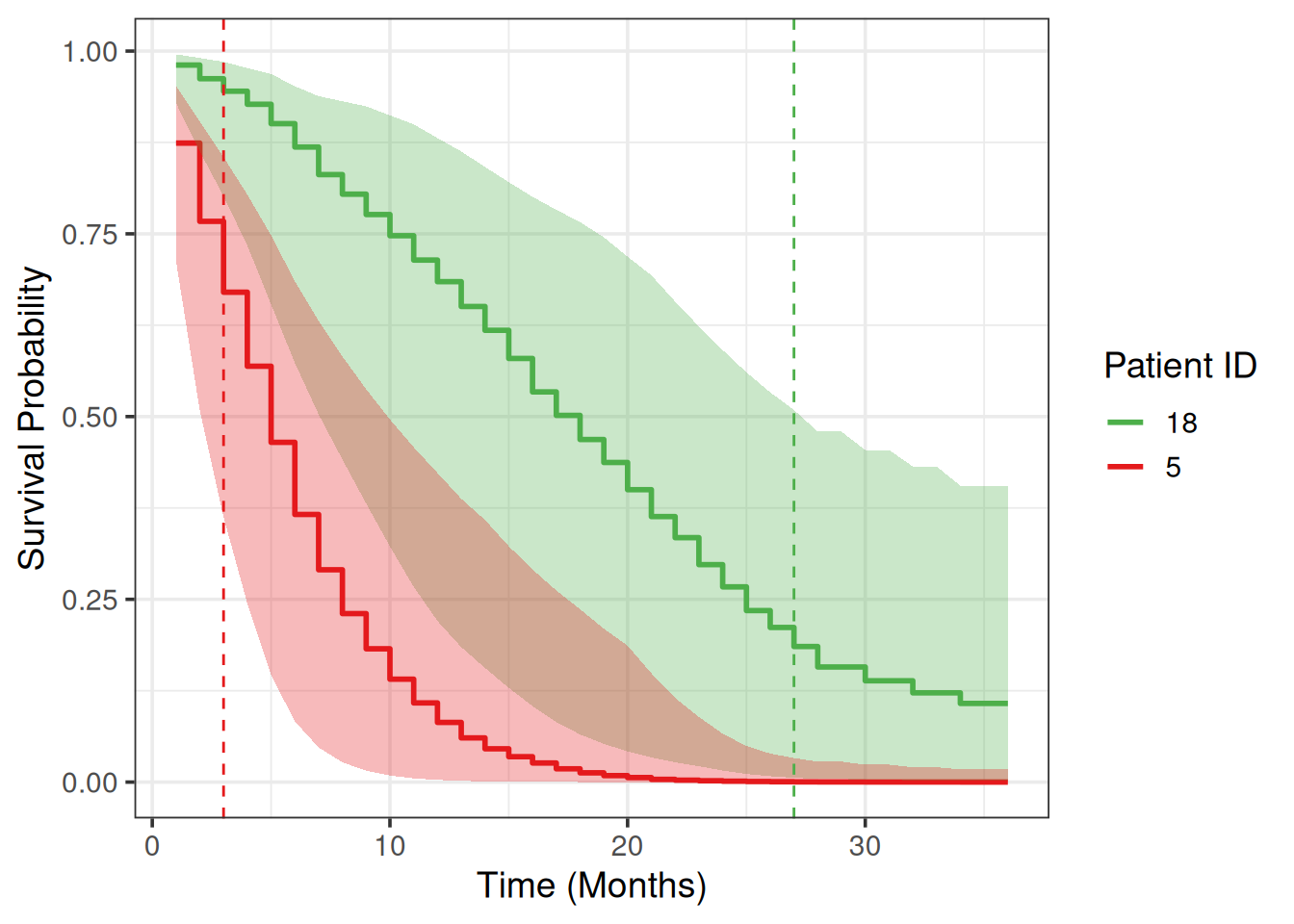

Uncertainty quantification for the survival prediction of two patients in the test set using 95% credible intervals. The two vertical lines correspond to the reported time of death (in months) for the two patients.

Partial Dependence Plot

We will use a Partial Dependence Plot (PDP) (Friedman 2001) to visualize how much different are males vs females in terms of their average survival predictions across time.

Note

PDPs assume that features are independent. In our case we need to check that sex doesn’t correlate with any of the other features used for training the BART learner. Since sex is a categorical feature, we fit a linear model using as target variable every other feature in the data (\(lm(feature \sim sex)\)) and conduct an ANOVA (ANalysis Of VAriance) to get the variance explained or \(R^2\). The square root of that value is the correlation measure we want.

# code from https://christophm.github.io/interpretable-ml-book/ale.html
mycor = function(cnames, data) {
  x.num = data[, cnames[1], with = FALSE][[1]]
  x.cat = data[, cnames[2], with = FALSE][[1]]
  # R^2 = Cor(X, Y)^2 in simple linear regression
  sqrt(summary(lm(x.num ~ x.cat))$r.squared)
}

cnames = c("sex")
combs = expand.grid(y = setdiff(colnames(d), "sex"), x = cnames)
combs$cor = apply(combs, 1, mycor, data = task$data()) # use the train set
combs
          y   x        cor
1      time sex 0.11338256
2    status sex 0.22105006
3       age sex 0.12814230
4  meal.cal sex 0.16813658
5 pat.karno sex 0.07075345
6   ph.ecog sex 0.01197613
7  ph.karno sex 0.01512325
8   wt.loss sex 0.17288403

sex doesn’t correlate strongly with any other feature, so we can compute the PDP:

# create two datasets: one with males and one with females
# all other features remain the same (use train data, 205 patients)
d = task$data(rows = part$train) # `rows = part$test` to use the test set

d$sex = 1
task_males = as_task_surv(d, time = 'time', event = 'status', id = 'lung-males')
d$sex = 0
task_females = as_task_surv(d, time = 'time', event = 'status', id = 'lung-females')

# make predictions
p_males   = learner$predict(task_males)
p_females = learner$predict(task_females)

# take the median posterior survival probability
surv_males   = p_males$distr$survival(months) # patients x times
surv_females = p_females$distr$survival(months) # patients x times

# tidy up data: average and quantiles across patients
data_males =
  apply(surv_males, 1, function(row) {
    tibble(
      low = quantile(row, probs = 0.025),
      avg = mean(row),
      high = quantile(row, probs = 0.975)
    )
  }) %>%
  bind_rows() %>%
  add_column(sex = 'male', month = months, .before = 1)

data_females =
  apply(surv_females, 1, function(row) {
    tibble(
      low = quantile(row, probs = 0.025),
      avg = mean(row),
      high = quantile(row, probs = 0.975)
    )
  }) %>%
  bind_rows() %>%
  add_column(sex = 'female', month = months, .before = 1)

pdp_tbl = bind_rows(data_males, data_females)
pdp_tbl
# A tibble: 72 × 5
   sex   month    low   avg  high
   <chr> <int>  <dbl> <dbl> <dbl>
 1 male      1 0.809  0.944 0.979
 2 male      2 0.652  0.892 0.958
 3 male      3 0.525  0.842 0.934
 4 male      4 0.411  0.792 0.911
 5 male      5 0.332  0.748 0.889
 6 male      6 0.240  0.686 0.851
 7 male      7 0.168  0.635 0.816
 8 male      8 0.120  0.579 0.775
 9 male      9 0.0777 0.523 0.728
10 male     10 0.0504 0.467 0.687
# ℹ 62 more rows
my_colors = c("#E41A1C", "#4DAF4A")
names(my_colors) = c('male', 'female')

pdp_tbl %>%
  ggplot(aes(x = month, y = avg)) +
  geom_step(aes(color = sex), linewidth = 1) +
  xlab('Time (Months)') +
  ylab('Survival Probability') +
  geom_ribbon(aes(ymin = low, ymax = high, fill = sex), alpha = 0.2, show.legend = F) +
  theme_bw(base_size = 14) +
  scale_color_manual(values = my_colors) +
  scale_fill_manual(values = my_colors)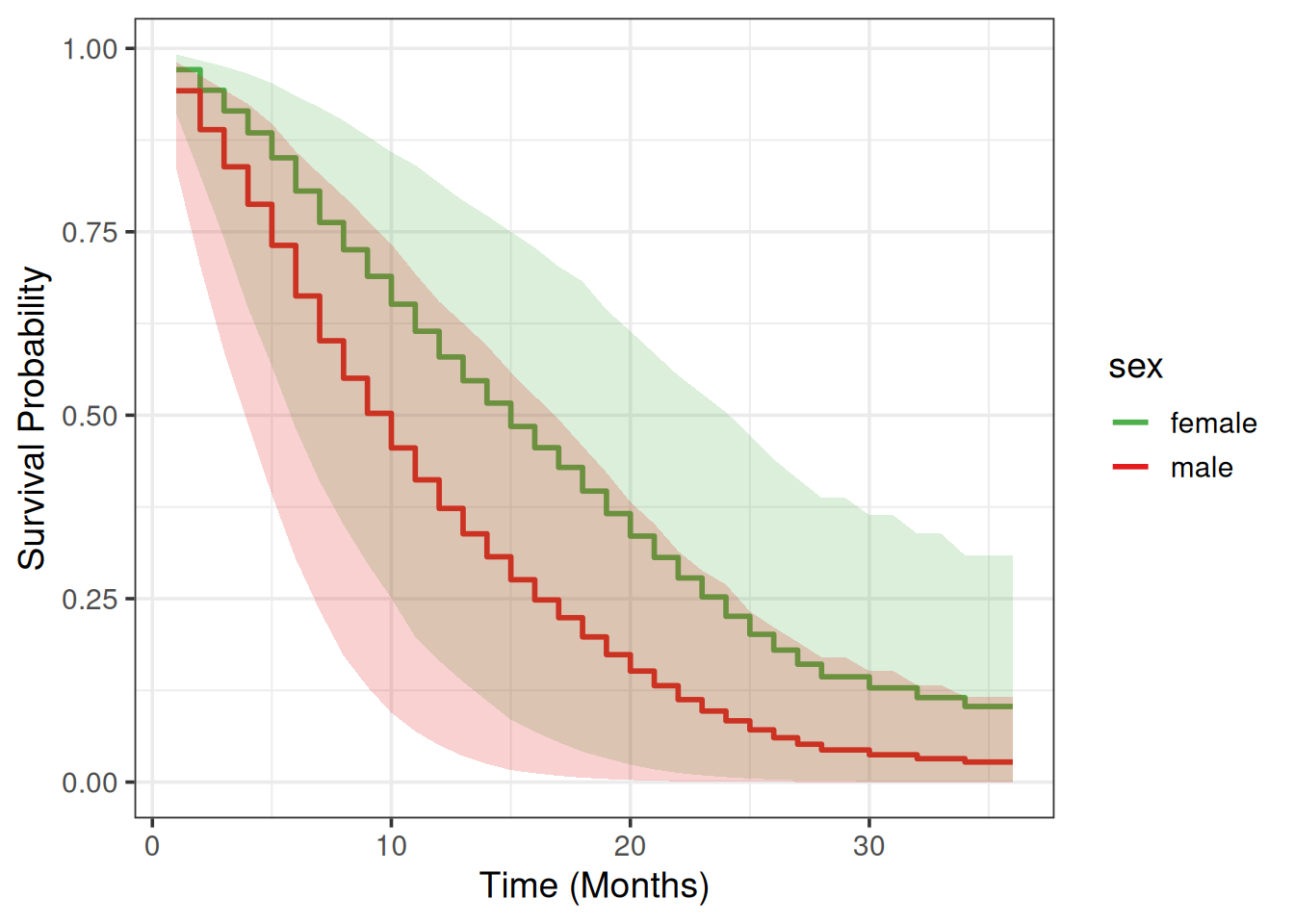

Friedman’s partial dependence function with 95% prediction intervals: males vs females. Females show on average larger survival estimates compared to men, across all time points. Overlapping shaded area represents men and women that have similar survival characteristics.

Session Information

sessioninfo::session_info(info = "packages")
═ Session info ═══════════════════════════════════════════════════════════════════════════════════════════════════════
─ Packages ───────────────────────────────────────────────────────────────────────────────────────────────────────────
 ! package           * version    date (UTC) lib source
   backports           1.5.0      2024-05-23 [1] CRAN (R 4.4.1)
   BART              * 2.9.9      2024-06-21 [1] CRAN (R 4.4.1)
   checkmate           2.3.2      2024-07-29 [1] CRAN (R 4.4.1)
   cli                 3.6.3      2024-06-21 [1] CRAN (R 4.4.1)
 P codetools           0.2-20     2024-03-31 [?] CRAN (R 4.4.0)
   colorspace          2.1-1      2024-07-26 [1] CRAN (R 4.4.1)
   crayon              1.5.3      2024-06-20 [1] CRAN (R 4.4.1)
   data.table        * 1.16.2     2024-10-10 [1] CRAN (R 4.4.1)
   dictionar6          0.1.3      2021-09-13 [1] CRAN (R 4.4.1)
   digest              0.6.37     2024-08-19 [1] CRAN (R 4.4.1)
   distr6            * 1.8.4      2024-10-17 [1] Github (xoopR/distr6@a642cd3)
   dplyr             * 1.1.4      2023-11-17 [1] CRAN (R 4.4.1)
   evaluate            1.0.1      2024-10-10 [1] CRAN (R 4.4.1)
   fansi               1.0.6      2023-12-08 [1] CRAN (R 4.4.1)
   farver              2.1.2      2024-05-13 [1] CRAN (R 4.4.1)
   fastmap             1.2.0      2024-05-15 [1] CRAN (R 4.4.1)
   future              1.34.0     2024-07-29 [1] CRAN (R 4.4.1)
   future.apply        1.11.2     2024-03-28 [1] CRAN (R 4.4.1)
   generics            0.1.3      2022-07-05 [1] CRAN (R 4.4.1)
   ggplot2           * 3.5.1      2024-04-23 [1] CRAN (R 4.4.1)
   globals             0.16.3     2024-03-08 [1] CRAN (R 4.4.1)
   glue                1.8.0      2024-09-30 [1] CRAN (R 4.4.1)
   gtable              0.3.5      2024-04-22 [1] CRAN (R 4.4.1)
   htmltools           0.5.8.1    2024-04-04 [1] CRAN (R 4.4.1)
   htmlwidgets         1.6.4      2023-12-06 [1] CRAN (R 4.4.1)
   jsonlite            1.8.9      2024-09-20 [1] CRAN (R 4.4.1)
   knitr               1.48       2024-07-07 [1] CRAN (R 4.4.1)
   labeling            0.4.3      2023-08-29 [1] CRAN (R 4.4.1)
 P lattice             0.22-5     2023-10-24 [?] CRAN (R 4.3.3)
   lgr                 0.4.4      2022-09-05 [1] CRAN (R 4.4.1)
   lifecycle           1.0.4      2023-11-07 [1] CRAN (R 4.4.1)
   listenv             0.9.1      2024-01-29 [1] CRAN (R 4.4.1)
   magrittr            2.0.3      2022-03-30 [1] CRAN (R 4.4.1)
 P Matrix              1.7-0      2024-04-26 [?] CRAN (R 4.4.0)
   mlr3              * 0.21.0     2024-09-24 [1] CRAN (R 4.4.1)
   mlr3extralearners * 0.9.0-9000 2024-10-18 [1] Github (mlr-org/mlr3extralearners@a622524)
   mlr3misc            0.15.1     2024-06-24 [1] CRAN (R 4.4.1)
   mlr3pipelines     * 0.7.0      2024-09-24 [1] CRAN (R 4.4.1)
   mlr3proba         * 0.6.9      2024-10-17 [1] Github (mlr-org/mlr3proba@45a5b79)
   mlr3viz             0.9.0      2024-07-01 [1] CRAN (R 4.4.1)
   mlr3website       * 0.0.0.9000 2024-10-18 [1] Github (mlr-org/mlr3website@20d1ddf)
   munsell             0.5.1      2024-04-01 [1] CRAN (R 4.4.1)
 P nlme              * 3.1-165    2024-06-06 [?] CRAN (R 4.4.0)
 P nnet              * 7.3-19     2023-05-03 [?] CRAN (R 4.3.3)
   ooplah              0.2.0      2022-01-21 [1] CRAN (R 4.4.1)
   palmerpenguins      0.1.1      2022-08-15 [1] CRAN (R 4.4.1)
   paradox             1.0.1      2024-07-09 [1] CRAN (R 4.4.1)
   parallelly          1.38.0     2024-07-27 [1] CRAN (R 4.4.1)
   param6              0.2.4      2024-10-17 [1] Github (xoopR/param6@0fa3577)
   pillar              1.9.0      2023-03-22 [1] CRAN (R 4.4.1)
   pkgconfig           2.0.3      2019-09-22 [1] CRAN (R 4.4.1)
   purrr               1.0.2      2023-08-10 [1] CRAN (R 4.4.1)
   R6                  2.5.1      2021-08-19 [1] CRAN (R 4.4.1)
   Rcpp                1.0.13     2024-07-17 [1] CRAN (R 4.4.1)
   renv                1.0.11     2024-10-12 [1] CRAN (R 4.4.1)
   rlang               1.1.4      2024-06-04 [1] CRAN (R 4.4.1)
   rmarkdown           2.28       2024-08-17 [1] CRAN (R 4.4.1)
 P rpart               4.1.23     2023-12-05 [?] CRAN (R 4.4.0)
   scales              1.3.0      2023-11-28 [1] CRAN (R 4.4.1)
   sessioninfo         1.2.2      2021-12-06 [1] CRAN (R 4.4.1)
   set6                0.2.6      2024-10-17 [1] Github (xoopR/set6@a901255)
 P survival          * 3.7-0      2024-06-05 [?] CRAN (R 4.4.0)
   tibble            * 3.2.1      2023-03-20 [1] CRAN (R 4.4.1)
   tidyr             * 1.3.1      2024-01-24 [1] CRAN (R 4.4.1)
   tidyselect          1.2.1      2024-03-11 [1] CRAN (R 4.4.1)
   utf8                1.2.4      2023-10-22 [1] CRAN (R 4.4.1)
   uuid                1.2-1      2024-07-29 [1] CRAN (R 4.4.1)
   vctrs               0.6.5      2023-12-01 [1] CRAN (R 4.4.1)
   withr               3.0.1      2024-07-31 [1] CRAN (R 4.4.1)
   xfun                0.48       2024-10-03 [1] CRAN (R 4.4.1)
   yaml                2.3.10     2024-07-26 [1] CRAN (R 4.4.1)

 [1] /home/marc/repositories/mlr3website/mlr-org/renv/library/linux-ubuntu-noble/R-4.4/x86_64-pc-linux-gnu
 [2] /home/marc/.cache/R/renv/sandbox/linux-ubuntu-noble/R-4.4/x86_64-pc-linux-gnu/9a444a72

 P ── Loaded and on-disk path mismatch.

──────────────────────────────────────────────────────────────────────────────────────────────────────────────────────

References

Bonato, Vinicius, Veerabhadran Baladandayuthapani, Bradley M. Broom, Erik P. Sulman, Kenneth D. Aldape, and Kim Anh Do. 2011. “Bayesian ensemble methods for survival prediction in gene expression data.” Bioinformatics 27 (3): 359–67. https://doi.org/10.1093/BIOINFORMATICS/BTQ660.
Chipman, Hugh A, Edward I George, and Robert E McCulloch. 2010. “BART: BAYESIAN ADDITIVE REGRESSION TREES.” The Annals of Applied Statistics 4 (1): 266–98. http://www.jstor.org/stable/27801587.
Friedman, Jerome H. 2001. “Greedy function approximation: a gradient boosting machine.” Annals of Statistics, 1189–1232. https://doi.org/10.1214/aos/1013203451.
Sonabend, Raphael, Andreas Bender, and Sebastian Vollmer. 2022. “Avoiding C-hacking when evaluating survival distribution predictions with discrimination measures.” Edited by Zhiyong Lu. Bioinformatics, July. https://doi.org/10.1093/BIOINFORMATICS/BTAC451.
Sonabend, Raphael, Florian Pfisterer, Alan Mishler, Moritz Schauer, Lukas Burk, Sumantrak Mukherjee, and Sebastian Vollmer. 2022. “Flexible Group Fairness Metrics for Survival Analysis,” May. https://doi.org/10.48550/arxiv.2206.03256.
Sparapani, Rodney A., Brent R. Logan, Robert E. McCulloch, and Purushottam W. Laud. 2016. “Nonparametric survival analysis using Bayesian Additive Regression Trees (BART).” Statistics in Medicine 35 (16): 2741–53. https://doi.org/10.1002/SIM.6893.
Sparapani, Rodney, Charles Spanbauer, and Robert McCulloch. 2021. “Nonparametric Machine Learning and Efficient Computation with Bayesian Additive Regression Trees: The BART R Package.” Journal of Statistical Software 97 (1): 1–66. https://doi.org/10.18637/JSS.V097.I01.